Une photo peut être précieuse et pourtant décevante : un visage mangé par le bruit en basse lumière, un paysage flou après un mouvement, un vieux JPEG “carré” récupéré d’une messagerie. Améliorer la qualité, ce n’est pas “mettre un filtre magique” : c’est une discipline qui mélange modélisation (comment l’image s’est dégradée), statistiques (ce qu’on suppose du bruit), optimisation (ce qu’on cherche à reconstruire) et, depuis quelques années, deep learning (ce que le modèle a appris du monde).
L’objectif de cet article est de rendre lisibles les grandes familles d’approches, avec quelques formules de référence et surtout l’intuition : pourquoi certaines méthodes font des merveilles sur un type d’images, et échouent sur d’autres.
Car la qualité n’est pas une valeur absolue, c’est un compromis entre fidélité, netteté perçue, artefacts, et respect de la scène originale.
Pourquoi une photo se dégrade-t-elle vraiment ?
On peut résumer une grande partie des “mauvaises photos” à quatre causes : bruit, flou, compression, et manque de résolution. Chacune correspond à une réalité physique ou numérique différente. Le bruit vient souvent du capteur et de la lumière : quand il fait sombre, le signal utile est faible, et les fluctuations aléatoires deviennent visibles. Le flou, lui, est souvent un mélange de bougé (vous ou le sujet), de mise au point imparfaite et de limites optiques. La compression, enfin, est un choix de stockage ou de transmission : on jette de l’information jugée “moins importante”, mais le prix peut être des blocs, du banding, des contours sales.
Le cas du JPEG est pédagogique : la norme repose sur une transformation en cosinus discrète (DCT) appliquée par blocs de 8 par 8, soit 64 coefficients par bloc, puis une quantification qui écrase davantage les hautes fréquences. C’est efficace pour alléger le fichier, mais cela peut produire l’aspect “mosaïque” et des artefacts sur les contours quand on compresse trop. Cette logique bloc par bloc fait partie de l’ADN du JPEG.
Repère : un modèle mental utile
Bruit = aléa ajouté au signal. Flou = mélange (étalement) du signal. Compression = perte volontaire d’information. Résolution = quantité d’échantillons disponibles.
Pour clarifier, les ingénieurs utilisent souvent une équation simple : l’image observée est l’image vraie, transformée par un système (optique, mouvement, compression), plus du bruit. Dit autrement : ce que vous voyez est une version dégradée d’une scène, pas “la scène” elle-même. Toute amélioration est donc une reconstruction : on essaie de remonter la pente, sans avoir toutes les informations.
Peut-on écrire une “équation de la photo ratée” ?
Une manière classique de poser le problème est : observation = (image nette convoluée par un noyau de flou) + bruit. La convolution, c’est le fait d’étaler chaque point selon une “empreinte” appelée PSF (point spread function). Un flou de bougé, par exemple, ressemble à un trait : l’empreinte est allongée, et l’image perd ses détails fins dans la direction du mouvement. Quand le noyau est connu ou approximable, on parle de déconvolution. Quand il est inconnu, on entre dans la “déconvolution aveugle”, nettement plus délicate.
La compression s’intègre aussi à ce schéma, mais de façon moins élégante : elle n’est pas juste un flou ou un bruit additif, c’est une opération non linéaire qui introduit des artefacts structurés (blocs, anneaux, bavures). C’est pour ça qu’un algorithme très bon contre le bruit gaussien peut être décevant sur une image surexploitée par une messagerie.
Dans la pratique, avant même de choisir une méthode, on gagne à diagnostiquer la dégradation dominante. Quelques questions simples aident :
- Le grain est-il fin et aléatoire, ou en gros pâtés colorés ?
- Les contours sont-ils doublés, “fantômes”, ou simplement mous ?
- Voyez-vous une grille de blocs ou des aplats avec des marches ?
- Le problème est-il partout, ou surtout dans les ombres et le ciel ?
Cette phase d’observation évite l’erreur classique : traiter une compression comme du bruit, ou un flou comme un manque de résolution.
Comment mesurer une amélioration sans s’auto-illusionner ?
Les images “plus nettes” peuvent être en réalité plus fausses. D’où l’usage de métriques. La plus simple est la MSE (mean squared error) : on calcule l’écart pixel par pixel entre l’original (référence) et la version restaurée, on met au carré, puis on moyenne. C’est clair, mais pas très “humain” : une petite translation ou un détail mal reconstruit peut exploser la MSE alors que l’image paraît correcte.
La PSNR (peak signal-to-noise ratio) est une reformulation en décibels : PSNR = 10 * log10( MAX² / MSE ). Pour une image 8 bits, MAX vaut 255, parce que le pixel le plus lumineux vaut 255. Des documents techniques standardisent ce calcul, notamment dans des recommandations utilisées côté vidéo où l’on fixe explicitement ce pic à 255² pour l’échelle 8 bits.
La SSIM (structural similarity) vise justement à coller davantage à la perception : elle compare des structures locales plutôt que des écarts bruts. L’idée a été popularisée dans un article très cité de Wang, Bovik, Sheikh et Simoncelli (IEEE Transactions on Image Processing, 2004), et c’est devenu un repère quasi standard dans les papiers de restauration et de super-résolution.
Repère : ce que disent ces métriques, en clair
MSE/PSNR mesurent “à quel point je suis proche des pixels de référence”. SSIM mesure “à quel point j’ai conservé la structure perçue”. Aucune ne détecte parfaitement une hallucination “plausible” d’un modèle.
Enfin, un point important : ces métriques supposent souvent qu’il existe une référence “vraie”. Dans la vraie vie, vous avez rarement l’original net. On bascule alors vers des critères sans référence (no-reference), et surtout vers une évaluation qualitative : texture naturelle, absence de halos, visages crédibles, pas de lettres inventées.
Quelles méthodes classiques marchent encore très bien ?
Le filtrage est la famille la plus ancienne et, dans beaucoup de cas, la plus rentable.
Le filtre moyen (moyenne locale) réduit le bruit mais floute.
Un filtre médian supprime bien certains parasites impulsionnels (pixels aberrants) tout en respectant mieux les contours.
Le filtre gaussien est un lissage doux, mais il efface vite les détails fins. Les filtres plus “intelligents”, comme le bilatéral, essaient de lisser dans les zones homogènes sans traverser les bords.
Dans une chaîne de traitement, il arrive qu’on doive redimensionner image avant d’appliquer certains filtres, parce que l’échelle change la perception du bruit et le coût de calcul. Le piège est de confondre “plus petit” avec “plus propre” : on a parfois simplement caché les défauts en réduisant les détails visibles, sans améliorer l’information.
À l’inverse, les méthodes dites “non locales” exploitent une observation simple : une image contient souvent des motifs répétés (texture d’un mur, feuillage, tissus). Le non-local means, proposé par Buades, Coll et Morel, compare des patchs semblables, même loin dans l’image, et moyenne de façon pondérée. Cela permet de réduire le bruit tout en préservant des structures répétitives, là où un filtre local aurait tout lissé.
C’est aussi le bon endroit pour comprendre une idée clé : les mêmes compromis existent en photo comme en vidéo. Si vous passez un fichier par un convertisseur mp4, vous voyez immédiatement le rôle de la compression : moins de débit, plus d’artefacts. En image fixe, c’est pareil : vous arbitrez toujours entre poids, détails et défauts visibles, même si l’outil ne s’appelle pas “codec”.
Déflouter et désartefacter : la déconvolution et l’optimisation
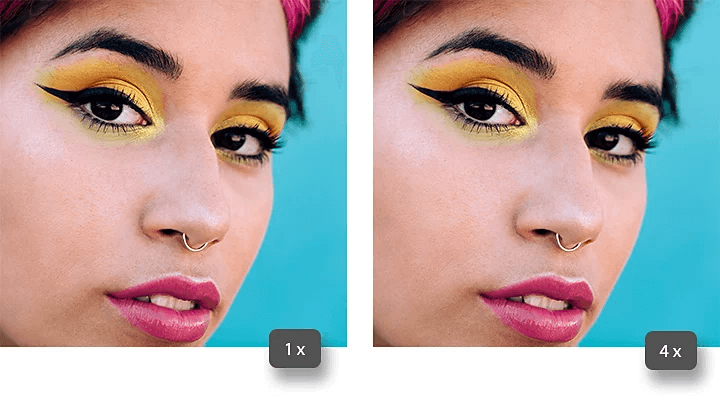
Quand le flou est modélisable, la déconvolution tente de l’inverser. Le filtre de Wiener est un classique : il cherche une estimation qui minimise l’erreur quadratique moyenne, en tenant compte d’un rapport signal sur bruit. Dit simplement, il “décide” de ne pas trop amplifier les fréquences où le bruit domine, sinon il créerait des oscillations et du grain artificiel. L’idée du Wiener, c’est une inversion prudente, pas un retour naïf à la netteté.
La déconvolution itérative de Richardson-Lucy est une autre grande référence, souvent utilisée quand on modélise un bruit de type Poisson (fréquent en imagerie scientifique). Son mécanisme peut se résumer ainsi : on part d’une estimation, on la “refloute”, on compare à l’observation, puis on corrige en redistribuant l’erreur via le noyau de flou. Cette correction se répète en boucle, et peut être très efficace, mais elle a aussi une réputation : si on itère trop, on amplifie le bruit et on crée des artefacts.
Quand on veut agrandir, la difficulté augmente : on essaie de fabriquer des détails absents. On peut redimensionner image avec une interpolation simple (bilinéaire, bicubique), mais c’est une reconstruction “géométrique” qui ne crée pas d’information nouvelle. Toute méthode plus ambitieuse doit introduire une hypothèse forte : “les images naturelles ressemblent statistiquement à ceci”. C’est là que l’optimisation et la régularisation entrent en scène.
La régularisation la plus connue est la variation totale (Total Variation). L’idée, introduite par Rudin, Osher et Fatemi (1992), est de chercher une image proche des données, mais dont la somme des variations locales (en gros, l’intensité des gradients) reste raisonnable. Concrètement, ça enlève le bruit dans les zones plates tout en gardant des bords nets, au prix parfois d’un effet “cartoon” si on pousse trop.
Même l’évaluation se rapproche de ces arbitrages. Si vous exportez, comparez, ré-encodez, puis repassez par un convertisseur mp4 pour une version vidéo, vous découvrez que la métrique (PSNR, SSIM) peut monter alors que l’image “fait bizarre”. C’est un rappel utile : un chiffre ne remplace pas un contrôle visuel, surtout quand des artefacts structurés entrent en jeu.
Dernier point souvent oublié : diminuer la résolution peut être un choix de qualité perçue. Dans certains cas, redimensionner image vers une taille plus petite, avec un bon ré-échantillonnage, donne un rendu plus propre qu’une restauration agressive qui invente des textures. Ce n’est pas une capitulation, c’est une stratégie : mieux vaut une photo cohérente et naturelle qu’une photo “sur-traitée”.
Et le deep learning dans tout ça : progrès réel, nouveaux risques
Le deep learning a changé l’échelle des résultats, surtout pour la réduction de bruit, la super-résolution et la suppression d’artefacts de compression. Au lieu de coder une règle (moyenner, préserver les bords, limiter les gradients), on entraîne un réseau sur des paires “dégradé propre” pour qu’il apprenne une fonction de restauration. Dans les meilleurs cas, les textures reviennent, les visages gagnent en lisibilité, et les blocs de compression disparaissent de façon impressionnante.
Mais l’avantage est aussi le danger : un réseau peut produire une image plausible, pas forcément fidèle. Sur un portrait, il peut lisser la peau “comme il a appris” au lieu de conserver la texture réelle. Sur du texte, il peut reconstruire des lettres fausses mais crédibles. La règle pratique est simple : plus l’image a une valeur documentaire (preuves, documents, médecine, recherche), plus on doit préférer des méthodes contrôlables et traçables, ou au minimum conserver l’original et documenter le traitement.
Dans un usage quotidien, le meilleur compromis est souvent hybride : un débruitage modéré, une correction de flou prudente, puis un contrôle à 100 % sur les zones sensibles (yeux, cheveux, lettres, motifs répétitifs). Et si l’image est destinée à une publication web ou à une diffusion, garder en tête la chaîne complète de recompression, y compris si vous devez ensuite produire une version animée ou passer par un convertisseur mp4, car chaque ré-encodage peut réintroduire des défauts.
Recommandations pour améliorer une photo sans la dénaturer
Avant de “booster” une image, posez un objectif concret : réduire le bruit, corriger un léger bougé, masquer des blocs de compression, ou rendre un visage plus lisible. Ensuite, adoptez une routine simple : travaillez sur une copie, comparez régulièrement avant/après à zoom identique, et vérifiez les zones à risque (contours, ciels, texte, peau). Enfin, méfiez-vous du réflexe “plus net = mieux” : les halos et la sur-accentuation sont souvent plus visibles que le défaut initial.
Questions de lecteur
Comment savoir si le problème principal est le bruit ou la compression ?
Le bruit ressemble souvent à un grain aléatoire, surtout dans les ombres. La compression crée plutôt des blocs, des aplats “en marches” et des contours sales.
PSNR et SSIM, est-ce indispensable ?
Non, sauf si vous comparez des algorithmes de façon rigoureuse. Pour un usage courant, c’est surtout utile pour éviter de se tromper quand deux résultats “semblent” proches.
Pourquoi le défloutage crée parfois des halos ?
Parce qu’inverser un flou amplifie aussi certaines fréquences et peut sur-accentuer les bords. Sans régularisation, on reconstruit autant le défaut que le détail.
Le deep learning peut-il inventer des détails ?
Oui. Il peut produire des textures plausibles mais inexactes, surtout sur les visages et le texte. Gardez toujours l’original et contrôlez les zones critiques.
